Update：我們的結果在https://arxiv.org/abs/2002.10646就被人證明過了QQ

———-

最近跟子超和吴茁的paper終於上arXiv了，這是我在IBS visit的時候的產物XD，János Pach丟給子超後我們三個討論的，最後靠著茁哥carry後做出來XD

講結果之前先來簡介一下背景知識。Erdős跟Szekeres證明了平面上給你足夠多in general position (平面上的話任三點不共線)的點，那總是可以找到一個凸的邊形。所以下個問題就是，那我能不能找到空的凸邊形，稱為convex -hole (凸洞(???))。結論是，答案是不行的，Horton給出了任意多點沒有-hole的構造，然後是最小滿足這件事的數字。聰明的讀者在這裡就會問出很多延伸問題，像是更高維度呢？的時候-hole最多可以有幾個啊？如果我只考慮格點啊？如果我把點塗色能不能找到同色的-hole啊？諸如此類的問題。

那第一個問題呢，正是我phd的第一個project。我們證明了在維的時候，對應的神奇數字上界是，但已知下界是線性的，雖然還是差很遠，但原本上界是。(請見：https://arxiv.org/abs/2007.08972)

回到現在這篇paper，這裡我們關心的問題是數-hole的個數，也就是空的三角形。

問題：給定平面上個任三點不共線的點，請問至少能找到幾個空的三角形？

而這個問題不難(如果只關心order的話)，答案是這個order，下界的話你考慮任兩點連線段與離他最近的點形成的三角形，上界留給讀者思考(?)。那如果我把點集合圖成紅色跟藍色呢？

問題：給定平面上個任三點不共線的點，個塗紅個塗藍，請問至少能找到幾個空的同色的三角形？幾個空的兩同一異的三角形？

前者是困難的，後者是簡單的XD，後者下界基本上是同一招，考慮一個紅藍連線段跟與他最近的點。但聰明的讀者會發現，這樣可能是紅紅藍也可能是紅藍藍三角形。那我如果限制只用一種呢？

問題：給定平面上個任三點不共線的點，個塗紅個塗藍，請問至少能找到幾個空的紅紅藍三角形？

試了很多構造後，還是會猜測是這個order。在我們的paper中，我們證明了至少有這個order這麼多個。證明大致概念如下：

1. 如果某個區域的紅色比藍色多很多，那總是可以找到很多要的三角形。
2. 如果從每個紅點連出去，紅色跟藍色都是很交錯的，那你也可以找到很多要的三角形。
3. 如果從某個紅點連出去，紅色跟藍色各自坨再一起的話，那你就可以製造出第一點要的某個區域。

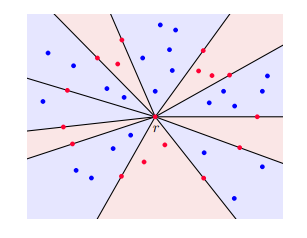
實際證明並沒有很長，還有我努力tikz的精美圖片XD，非常建議有空當休閒讀物看看(?) (請見：https://arxiv.org/abs/2409.17078)