最近跟眼皮把彩虹三角形的純entropy做法的note放到arXiv上了,於是想說來介紹一下我們這部分在幹麻。
我們先考慮以下的看起來是數奧的問題:給你一個簡單圖,假設他有
條紅邊、
條綠邊、
條藍邊,請問最多能有幾個彩虹三角形(三條邊顏色都不同的三角形)。
首先我們想一下構造,如果你有坨
個點,坨與坨之間只用一種顏色相連,這樣你會有
,並且有
個彩虹三角形,也就是說彩虹三角形個數是
。但其實考慮以下構造(blow-up of
)的話會有
且彩虹三角形個數是
。
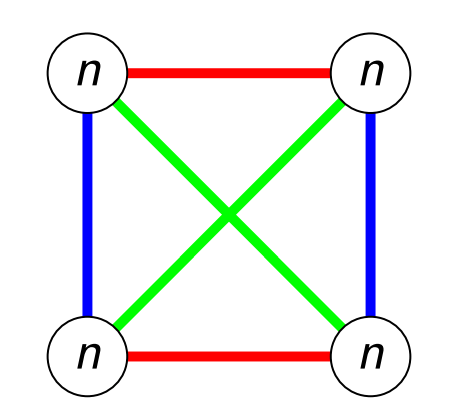
那接下來就會問說,這個構造是不是最好的?假設彩虹三角形個數是,我們能不能證明
?答案是可以的!
用數奧的講法,你可以考慮一個叫做Shannon entropy的神奇賦值。假設我給你一個值域有限的隨機變數,我可以定義他的entropy為
並類似的定義為
這個隨機變數的entropy,以此類推。則我們知道
(
是
的值域),且等號發生在
是均勻隨機的時候。
並且我們會有Shearer’s不等式
如果你均勻隨機的sample一個彩虹三角形,並讓
是紅邊,
是綠邊、
是藍邊,那你就會有
其中第一個等號跟最後一個不等號用到上面提到的值域的不等式,中間的不等號是Shearer’s不等式。注意到因為是有順序的,所以你只能用
壓他。然而這樣給出來的只有
,所以我們實際上還得把Shearer’s不等式好好拆開來看裡面哪一步鬆掉了好好跟他打架。這也是我們在這兩篇paper
https://arxiv.org/abs/2307.15379
https://arxiv.org/abs/2407.14084
在做的事情。第一篇基本上是喝醉的時候炸出來的,所以有些奇妙地從entropy跑回機率或是數數的世界。於是我們訪問MIT的時候,Yufei說他不喜歡這個證明,能不能有個純粹的entropy證明。於是我們就生出了第二篇的這個證明,其中的一步關鍵步是你要考慮一個莫名其妙(X)神來一筆(O)的injection並用到entropy在injection下是保持的,有興趣的讀者建議看看第二篇。
接下來來稍微講點為什麼這個問題有趣好了。首先有個經典的問題叫做joints problem,問你說在三維空間中,如果給你條線,你最多可以有幾個點是三條不共平面的線的交點。然後數學家看到線就想塗色,所以你可以考慮他的變體(multijoints problem):我給你
條紅線、
條綠線、
條藍線,那你最多可以有幾個點是三條不共平面的線的交點且這三條線顏色不同(稱為multijoints)?
有沒有覺得這看起來很熟悉?如果考慮我拿個位置很general的平面,每個平面代表圖上的一個頂點。那兩兩相交會是一條線,也就是說圖上的每條邊會對應到空間中的一條線。三個相交會是一個點,所以圖上的三個頂點會給你空間中的一個點。而空間中的這個點是一個multijoints若且唯若他們對應到的三個頂點形成一個彩虹三角形,也就是說彩虹三角形問題是multijoints問題的一個特例。
然而在multijoints問題中最好的界是,構造則是用上面那個圖給出來的
,所以我們想問說哪邊才是真理,於是先考慮圖上的版本。

發表留言